SquareRoots: Game of Guesses

April 20, 2021

Initially, we might feel like this is a really tough problem and even feel at loss to find out from where to start. But still to find out a solution we must think of the problem with a cool mind.

Naive Approach

So, let’s see the naive approach to solve this problem. We can take a smaller number than the given and keep guessing and squaring the number to check if we got the answer. For example, if given number is 25, we might start from 2 or 9 and start guessing and checking

\(2*2 = 4\)	\(9*9 = 81\)
\(3*3 = 9\)	\(8*8 = 64\)
\(4*4 = 16\)	\(7*7 = 49\)
\(5*5 = 25\)	\(6*6 = 36\)

Mentos Approach

In naive approach, the algo is as good as our initial guess only. For example, for 10,000 if our initial guess is 500 then it will take us around 400 iterations to converge upon the answer. So, what can be done in order to avoid this. From naive approach we can see that if our initial guess was too far off, we can derive one that is small enough.

Now, we can work on 2 of our initial guesses which were 2 and 9 i.e. it must lie between \(2*2 = 4\) and \(9*9 = 81.\) Taking

\[(2+9)/2 = 5.5\] \[25/5.5 = 4.54\] \[(5.5+4.54)/2 = 5.02\]

And just like that we can start converging towards the answer.

Kind of like from one guess, another guess is derived and slowly they converge towards the answer. Now taking this same algorithm and applying this for 10,000 we can see that it can be solved very quickly and breaking down the runtime from 400 to just 11 iterations.

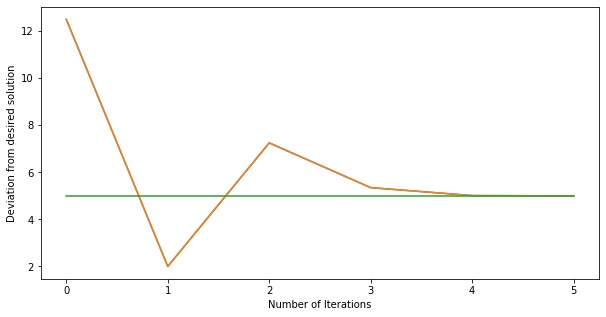Oscillating convergence to square root

Implementation

We can also implement this algorithm using python as below:

def findSqrt(m,e=4):
	''' Takes number n and e and returns squareroot of n to error e>12
	default error e = 4'''
	if m <= 0 or e > 12:	# negative or zero number case
		return 0
	g1 = m/2	# Guess 1
	if g1*g1 == m:
		return g1
	else:
		g2 = m/g1 # Guess 2
		# loop where guesses converge to the answer
		while round(g2*g2, e) != m or g1 == g2: # for common error elimination
			g1 = g2
			g2 = (g1 + (m/g1))/2
		return round(g2,e)

# Driver Code
n = float(input("Enter your number: "))
print(findSqrt(n))	

Input	\(25\)
Output	\(5\)

---